FDERIV

Updated 2023-10-18 20:35:52.667000

Syntax

SELECT [westclintech].[wct].[FDERIV] (
   <@Func, nvarchar(max),>
  ,<@VarName, nvarchar(4000),>
  ,<@X, float,>
  ,<@N, int,>
  ,<@H, float,>
  ,<@Meth, nvarchar(4000),>)

Description

Use the scalar function FDERIV for function differentiation for orders n = 1 to 8 using finite difference approximations.

Arguments

@N

Order of derivative, should only be between 1 and 8; for n = 0 function values will be returned.

@H

Step size

@VarName

The name of the variable.

@Meth

‘C’, ‘B’, or ‘F’ for central finite difference, backward finite difference, or forward finite difference

@X

The starting value for the evaluation.

@Func

The function to be evaluated, as a string. The function must be in the form of a SELECT statement.

Return Type

float

Remarks

If Func returns a NULL then NULL Is returned.

If Func is not a valid SELECT statement then NULL is returned.

If no solution is found then NULL is returned.

If X is NULL then X = 0.

If N is NULL then N = 1.

If H is NULL then H = 0.

If Meth is NULL then Meth = 0.

If H <= 0 then H =

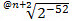
Examples

Example #1 Calculate f(x) as sin x, d(sin x)/dx, and cos x

SELECT SIN(PI() / 4) as [sin x],
       wct.FDERIV('SELECT SIN(@x)', '@x', PI() / 4, 1, NULL, 'B') as [d(sin x)/dx],
       COS(PI() / 4) as [cos x];

This produces the following result.

{"columns":[{"field":"sin x","headerClass":"ag-right-aligned-header","cellClass":"ag-right-aligned-cell"},{"field":"d(sin x)/dx","headerClass":"ag-right-aligned-header","cellClass":"ag-right-aligned-cell"},{"field":"cos x","headerClass":"ag-right-aligned-header","cellClass":"ag-right-aligned-cell"}],"rows":[{"sin x":"0.707106781186547","d(sin x)/dx":"0.70710678116969","cos x":"0.707106781186548"}]}

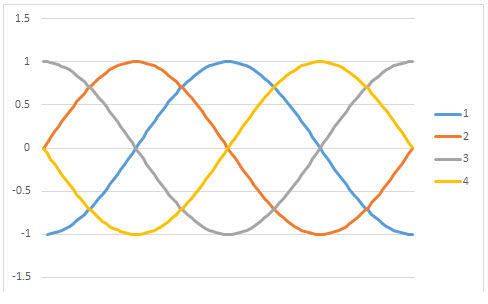
Example #2

Calculate the 1st through 4th derivatives of sin x from -PI to PI and paste the results in a Excel PivotChart.

SELECT n.n,

       SeriesValue,

       wct.FDERIV('SELECT SIN(@x)', '@x', SeriesValue, n.n, NULL, '22')

FROM wct.SeriesFloat(-PI(), PI(), .02 * PI(), NULL, 'L')

    CROSS APPLY

(

    VALUES

        (1),

        (2),

        (3),

        (4)

) n (n);