RANDBINOM

Updated 2023-10-18 15:33:07.660000

Syntax

SELECT * FROM [westclintech].[wct].[RANDBINOM](
  <@Rows, int,>
 ,<@p, float,>
 ,<@Trials, int,>)

Description

Use the table-valued function RANDBINOM to generate a sequence of random integers from the binomial distribution for a given probability of success @p and a given number of trials @Trials.

Arguments

@p

the success probability in each trial. @p must be of the type float or of a type that implicitly converts to float.

@Rows

the number of rows to generate. @MaxIterations must be of the type int or of a type that implicitly converts to int.

@Trials

the number of trials. @Trials must be of the type int or of a type that implicitly converts to int.

Return Type

table

{"columns": [{"field": "colName", "headerName": "Name", "header": "name"}, {"field": "colDatatype", "headerName": "Type", "header": "type"}, {"field": "colDesc", "headerName": "Description", "header": "description", "minWidth": 1000}], "rows": [{"id": "8e9a1f14-0deb-417c-85d5-1f087bf1e576", "colName": "Seq", "colDatatype": "int", "colDesc": "A monotonically increasing sequence number"}, {"id": "2def7bb4-fbf8-443a-8600-6017139d8b3e", "colName": "X", "colDatatype": "float", "colDesc": "The random variable"}]}

Remarks

@p must be greater than or equal to zero and less than or equal to 1 (0 <= @p <= 1).

@Trials must be greater than zero.

If @p is NULL then @p is set to 0.

If @Trials is NULL then @Trials is set to 1.

If @Rows is less than 1 then no rows are returned.

Examples

In this example we create a sequence 1,000,000 random numbers from a binomial distribution with @p = 0.3 and @Trials = 500, COUNT the results, paste then into Excel and graph them.

SELECT X,

       COUNT(*) as [COUNT]

FROM

(

    SELECT X

    FROM wct.RANDBINOM(   1000000, --@Rows

                          0.3,     --@p

                          500      --@Trials

                      )

) n

GROUP BY X

ORDER BY 1;

This produces the following result.

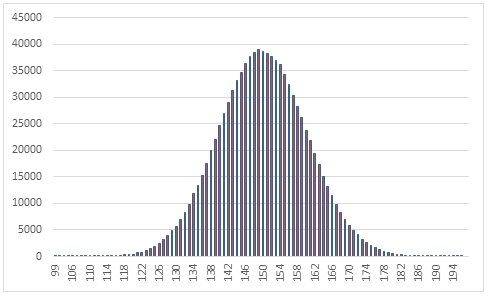
In this example we generate 1,000,000 random numbers from a binomial distribution with probability of .70 and number of trials = 140. We calculate the mean, standard deviation, skewness, and excess kurtosis from the resultant table and compare those values to the expected values for the distribution.

DECLARE @size as int = 1000000;
DECLARE @p as float = 0.70;
DECLARE @trials as float = 140;
DECLARE @mean as float = @p*@trials;
DECLARE @var as float = @mean*(1e+00-@p);
DECLARE @stdev as float = SQRT(@var);
DECLARE @skew as float =(1 - 2*@p)/@stdev;
DECLARE @kurt as float =(1-6*@p*(1e+00-@p))/@var;
 
SELECT
   stat,
   [RANDBINOM],
   [EXPECTED]
FROM (
   SELECT
      x.*
   FROM (
      SELECT
         AVG(cast(x as float)) as mean_BINOM,
         STDEVP(x) as stdev_BINOM,
         wct.SKEWNESS_P(x) as skew_BINOM,
         wct.KURTOSIS_P(x) as kurt_BINOM
      FROM
         wct.RANDBINOM(@size,@p,@trials)
      )n
   CROSS APPLY(
      VALUES
         ('RANDBINOM','avg', mean_BINOM),
         ('RANDBINOM','stdev', stdev_BINOM),
         ('RANDBINOM','skew', skew_BINOM),
         ('RANDBINOM','kurt', kurt_BINOM),
         ('EXPECTED','avg',@mean),
         ('EXPECTED','stdev',@stdev),
         ('EXPECTED','skew',@skew),
         ('EXPECTED','kurt',@kurt)
      )x(fn_name,stat,val_stat)    
   )d
PIVOT(sum(val_stat) FOR fn_name in([RANDBINOM],[EXPECTED])) P;

This produces the following result (your result will be different).

{"columns":[{"field":"stat"},{"field":"RANDBINOM","headerClass":"ag-right-aligned-header","cellClass":"ag-right-aligned-cell"},{"field":"EXPECTED","headerClass":"ag-right-aligned-header","cellClass":"ag-right-aligned-cell"}],"rows":[{"stat":"avg","RANDBINOM":"97.989814","EXPECTED":"98"},{"stat":"kurt","RANDBINOM":"-0.00503179349084126","EXPECTED":"-0.00884353741496599"},{"stat":"skew","RANDBINOM":"-0.0764751418091853","EXPECTED":"-0.0737711113563317"},{"stat":"stdev","RANDBINOM":"5.422481742284","EXPECTED":"5.42217668469038"}]}