GAMMALN

Updated 2024-03-08 15:41:24.717000

Syntax

SELECT [westclintech].[wct].[GAMMALN] (
   <@Z, float,>)

Description

Use the scalar function GAMMALN to calculate the natural logarithm of Γ(z). The GAMMA function can be defined as a definite integral for ℜ[z] > 0.

\Gamma(z) = \int_0^\infty t^{z-1} e^{-t}\,dt

Arguments

@Z

The value of interest.

Return Type

float

Remarks

GAMMA is undefined for negative integers.

GAMMA is undefined for zero.

Examples

Example #1

SELECT wct.GAMMALN(2.5) as Gammaln;

This produces the following result.

{"columns":[{"field":"Gammaln","headerClass":"ag-right-aligned-header","cellClass":"ag-right-aligned-cell"}],"rows":[{"Gammaln":"0.28468287047291"}]}

Example #2

SELECT LOG(wct.GAMMA(-3.75)) as Gammaln;

This produces the following result.

{"columns":[{"field":"Gammaln","headerClass":"ag-right-aligned-header","cellClass":"ag-right-aligned-cell"}],"rows":[{"Gammaln":"-1.31726794244636"}]}

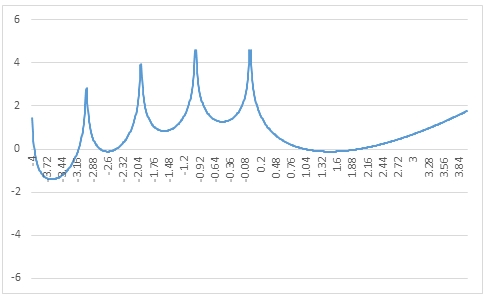
Example #3

The following SQL can be run using the SeriesFloat function to create GAMMALN values from -4 to 4 which can then be pasted into Excel and graphed.

SELECT z,

       wct.GAMMALN(z) as Gammaln

FROM

(

    SELECT SeriesValue as z

    FROM wct.SeriesFloat(-4, 4, 0.01, NULL, NULL)

) n;

This produces the following result.

See Also

DIGAMMA - Calculate digamma(z), the logarithmic derivative of the gamma function.

FACT - factorial of a number

FACTLN - natural logarithm of a factorial

GAMMA - complete gamma function

TRIGAMMA - trigamma function; the second derivative of the gamma function