In applied statistics there are times when you want to take your sample data and estimate the parameters of the distribution that best describes it. Without going too deeply into the math we look at how to fit a gamma distribution to the data. Specifically, we are trying to find the alpha and beta parameters to pass to the GAMMADIST function to calculate the probability density function. Doing this on the database is interesting because 1) that’s where our data is and 2) it makes it easy to include the calculation in work flows where, for example, we might want to do predictive analytics. Plus, it’s interesting and pretty easy to do. The focus of the fitting function is on the alpha (α) parameter as the beta (β) parameter can be calculated directly from α. 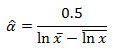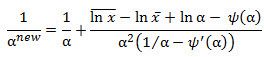The initial estimate for α is  The update step is  where ψ is the digamma function and ψ′ is the trigamma function. Let’s look at our SQL Server implementation. First, let’s declare some variables ``` DECLARE @tol as float = 0.00000001490116119384765625; DECLARE @xbar as float; DECLARE @logxbar as float; DECLARE @meanlogx as float; ``` Use a recursive CTE to calculate the alpha parameter of the gamma distribution. In this CTE we want to keep track of the number of iterations, the value of alpha and an error term. The number of iterations starts at 0 and terminates at 100. The initial value of alpha is as described above. The error term is simply the absolute value of the change in alpha |α(n+1)-αn|. We will initialize the error term to 1 and then iterate until the error term is less than the tolerance (defined above) or we have reached the maximum number of iterations. The anchor part of our CTE looks like this: ``` SELECT 0 as iter ,0.5 / (@logxbar - @meanlogx) as alpha ,1e+00 as err ``` The recursive part of the CTE does three things. First, it increments the iter column by 1. Second, the alpha column incorporates the update equation described above using the XLeratorDB DIGAMMA and TRIGAMMA functions. Third, the err column is populated as the absolute value of the difference between the current alpha value and the alpha value from the previous iteration. ``` SELECT n.iter + 1 ,n.alpha1 ,ABS(n.alpha1 - n.alpha0) as err FROM ( SELECT iter, alpha, 1/(1/alpha + (@meanlogx - @logxbar + LOG(alpha) - wct.digamma(alpha))/(POWER(alpha,2)*(1/alpha-wct.trigamma(alpha)))) FROM x WHERE err > @tol ``` This produces the following result. ``` iter alpha err ----------- ---------------------- ---------------------- 0 4.980636566422 1 1 5.14132956453772 0.160692998115715 2 5.14148887676296 0.000159312225243902 3 5.14148887691005 1.47081458123921E-10 ``` As you can see, the [fitting algorithm came with an alpha parameter](link) of 7.35 and a beta parameter 0.48 compared to values of 7.0 and 0.5 which were used to generate the sample data. Obviously, the larger the sample size, the better the fit will be. >In our testing the fit always happens in less than 5 iterations and in no measurable clock time. Your results will depend on your configuration, but this really isn’t a very expensive calculation at all.